I Diagrammer og Statistik værkstedet kan du visualisere data i mange forskellige diagramtyper, undersøge data, lave kurvetilpasning, deskriptiv statistik og hypotesetest.
Diagrammer og Statistik er meget tæt forbundet med Lister og Regneark, og tilføjer du et Diagrammer og Statistik værksted til et tomt dokument, så får du blot at vide, at der ikke er nogen lister til stede. Start derfor altid i Lister og Regneark.
Boxplot
Man har observeret 16 bilers hastighed gennem en by, hvor den højest tilladte hastighed er 50 km/t. De observerede hastigheder var:
70,\enspace 61,\enspace 55,\enspace 60,\enspace 52,\enspace 49,\enspace 72,\enspace 54,\enspace 48,\enspace 53,\enspace 47,\enspace 62,\enspace 49,\enspace 51,\enspace 52,\enspace 50
Tegn boxplottet for denne fordeling.
Tast hastighederne ind i en kolonne i et Lister og Regneark værksted. Navngiv kolonnen hastighed så den bliver tilgængelig i Diagrammer og Statistik værkstedet.
Tilføj herefter et Diagrammer og Statistik værksted, og knyt hastighed til x-aksen:
Højre-klik i arbejdsområdet, vælg Boxplot i menuen, og boxplottet tegnes. Ved at flytte markøren til boxplottets linjer, kan du få oplyst kvartilsættet:
Du kan plotte middelværdien sammen med et boxplot 
4:Undersøg data \rightarrow 8:Plot værdi. Indtast mean(hastighed) i det indtastningsfelt, der kommer frem:
Du kan let skifte mellem de forskellige plottyper: Prikplot, Boxplot, Histogram og Normalfordelingsplot. Nedenfor er vist det standard histogram, TI-Nspire leverer.
Hvis du ønsker større intervaller i histogrammet, kan du gribe og trække i skillelinjerne — eller lave (mere præcise) indstillinger ved at kalde histogrammets kontekstmenu frem ved at højre-klikke, og vælge 5:Søjleindstillinger.
Benyt 
til at indsætte variablen ’hastighed’
Boxplot efter en hyppighedsliste
Et matematikhold fik til skriftlig eksamen følgende karakterer:
Tegn boxplot for denne fordeling.
Opret et nyt Lister og Regneark værksted. Indtast tabellens oplysninger som vist nedenfor:
Vælg 
3:Data \rightarrow 8:Kombinationsdiagram. Indstil dialogen som vist, og tast Enter. Du vil da få tegnet et stolpediagram på en ny side. Højreklik for at ændre graftypen til boxplot:
Sammenligning af boxplot
I to klasser er fraværet for et kvartal opgjort til:
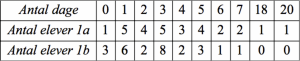
Sammenlign fraværet i de to klasser ved at tegne boxplot for begge.
Indtast data i et Lister og Regneark værksted, navngiv kolonnerne og marker hele dataområdet:
Vælg 
3:Data \rightarrow 8:Kombinationsdiagram. Indstil dialogen som vist, og tast Enter. Du vi da få tegnet de to stolpediagrammer på samme nye side. Højreklik for at ændre graftypen til boxplot.
Observationerne 18 og 20 er atypiske, og afsættes derfor som isolerede punkter. Ved at vælge 
2:Diagramegenskaber \rightarrow 3:Udvid boxplotgrænser kan du få punkterne forbundet.
\chi \, ^2-test for uafhængighed
En forretningskæde vil undersøge, om farven på indpakningen af nye kartofler påvirker salget. Butikken sælger derfor i en periode poser med samme slags kartofler, alle med 2,5 kg/pose og til samme pris.
Der bliver i alt sendt 600 poser kartofler ud i butikkerne, hvoraf 520 bliver solgt. Af de solgte poser er 375 gule, og der er 55 gule poser tilbage. De øvrige poser er blå.
Undersøg, om der er grundlag for at påstå, at farven påvirker salget af kartofler.
Først skal du lige vha. lidt hovedregning regne ud, at der er solgt 145 blå poser, og der er 25 blå poser tilbage. Indtast oplysningerne i et Lister og Regneark værksted:
Du skal afgøre, om de oplyste data er i rimelig overensstemmelse med nulhypotesen om uafhængighed mellem farve og antal solgte poser. Hertil skal du benytte det indbyggede test for uafhængighed af to variable.
Testen kan klares direkte i Lister og Regneark, vælg 
4:Statistik \rightarrow 4:Statistiske tests… \rightarrow 8:X2uafhængighedstest…. Guiden forventer, at du indtaster navnet på en matrix med observationerne. Dette kan du klare ved at indtaste {gul,blå}, tuborgklammer { og } kommer når man holder Shift+Alt 8 og Shift+Alt 9 inde.
Resultatet er følgende
- \chi \, ^2 – teststørrelsen har værdien 0.38672
- p-værdien er 53.4%, dvs. sandsynligheden for at finde en teststørrelse, der er mindst lige så skæv som den observerede, er 53.4%. Nulhypotesen accepteres altså på signifikansniveauet 5%.
- Teststørrelsen er \chi \, ^2 – fordelt med 1 frihedsgrad.
De forventede værdier finder du i matricen ExpMatrix og enkeltbidragene til X2-teststørrelsen finder du i CompMatrix. Vil du se de to matricer, sker det nemmest i et Noter værksted, hvor de hentes via 
knappen eller blot skrives vha. stat.:
Du får ikke oplyst den kritiske værdi for en test på signifikansniveau 5%. Skal du bruge denne, må du selv beregne den. Hertil skal du benytte den inverse \chi \, ^2-fordeling med 1 frihedsgrad. Du kan foretage beregningen i såvel Noter som i Lister og Regneark.
Vælg 6:Beregninger \rightarrow 6:Statistik \rightarrow 5:Fordelinger \rightarrow 9:inversX2, og indtast som vist:
Dette viser, at den kritiske værdi er 3.84.
\chi \, ^2-test for Goodness of Fit
Med \chi \, ^2-test Goodness of Fit kan du undersøge, om et observeret datasæt følger en forventet fordeling. Dette illustreres i følgende eksempel.
En mindre restaurant med et menukort bestående af 5 forskellige, men faste menuer plejer at have følgende ordrefordeling på disse:
menu 1: 30 %, menu 2: 25 %, menu 3: 20 %, menu 4: 15 % og menu 5: 10 %.
Restauranten foretager sine indkøb for at imødegå en efterspørgsel, der følger dette mønster. Imidlertid er man flere gange i den seneste tid løbet tør for menu 5, og man ønsker at afgøre, om det er en tilfældighed, eller om man skal revidere indkøbsplanerne.
I den seneste uge har man haft 543 gæster. Af disse bestilte 152 menu 1, 101 bestilte menu 2, 110 bestilte menu 3, 91 bestilte menu 4 og 89 bestilte menu 5.
Skal man revidere indkøbsplanerne?
Hypotesen H_0 er her, at ordrefordelingen i den sidste uge (stikprøven) ikke adskiller sig signifikant fra den sædvanlige ordrefordeling. Dvs., at den forventede ordrefordeling blandt de 543 gæster kan beregnes vha. de givne procenter.
Opret et nyt Lister og Regneark værksted, tast oplysningerne ind og beregn de forventede værdier (med en celleformel):
Vælg her 4:Statistik \rightarrow 4:Statistiske tests… \rightarrow 7:X2 Goodness of Fit test. Guiden forventer, at du giver navnet på en liste med observerede værdier (obs), en liste med forventede værdier og antallet af frihedsgrader (“antal rækker” – 1 = 4):
Resultatet af ovenstående udregning er, at p-værdien her er meget lille (0.000001), så lille, at restauranten må tage deres indkøbsplaner op til revision.
Deskriptiv statistik
En virksomhed producerer små metalaksler, hvis længde varierer mellem 10 og 20 mm. Der udtages 40 aksler af produktionen, og deres længde måles. De 40 målinger er grupperet i nedenstående intervaller
Find middelværdi og spredning, og undersøg, om observationerne kan antages at være normalfordelte.
Åbn et nyt dokument, og indsæt et Lister og Regneark værksted. Du kan ikke indtaste intervaller i en kolonne, så indtast i stedet intervalmidtpunkterne i kolonne A og hyppighederne i kolonne B. Navngiv kolonnerne som vist nedenfor.
Vælg nu 
4:Statistik \rightarrow 1:Statistiske beregninger… \rightarrow 1:Statistik med én variabel
Først kommer et lille vindue frem, hvor du skal angive, hvor mange lister, der skal indgå i statistikken. Vælg her 1. Indstil som vist nedenfor, og statistikken er klar:
I listen kan du se middelværdien (15.25), og bladrer du ned i listen, kan du blandt meget andet finde spredningen samt kvartilsættet (der i øvrigt ikke kan bruges til noget her, da data er samlet i interval midtpunkterne).
For at afbilde data i et histogram vælger du 
3:Data \rightarrow 8:Kombinationsdiagram. Indstil som vist på skærmbilledet nedenfor til venstre:
For at få den rette bredde på søjlerne, skal du kalde kontekstmenuen for søjlerne frem. Det gør du ved at højreklike hvor som helst på diagrammet. Vælg her 2:Søjleindstillinger \rightarrow 1:Lige store intervaller, og sæt bredden til 2 og søjlestart til 10. Så får du et histogram som på skærmbilledet ovenfor.
Du skal nu plotte sandsynlighedsfordelingen for normalfordelingen sammen med histogrammet. Vælg 
4:Undersøg data \rightarrow 9:Vis normal PDF.
Af skærmbilledet kan du se, at det er funktionen/kommandoen normPdf med middelværdi 15.25 og spredning 2.36115, der er tegnet.
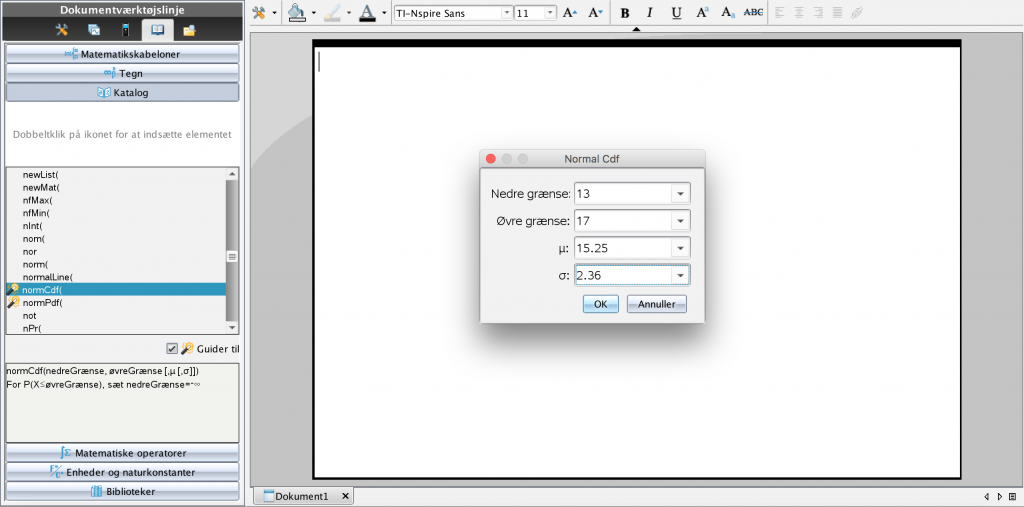
Antag, at længden af metalakslerne er normalfordelt med middelværdi \mu=15.25 og spredning \sigma=2.36.
Hvor mange procent af metalakslerne har en længde mellem 13mm og 17mm?
Indsæt et Noter værksted, og hent normCdf i kataloget eller blot indtast normCdf. Udfyld som vist, og du finder, at ca. 60% af metalakslerne har en længde mellem 13mm og 17mm:
NormCdf er den kumulerede fordelingsfunktion for normalfordelingen.
Du kan komme frem til dette resultat på mange måder. Husk, at det, der skal bestemmes, er arealet under normalfordelingen (normPdf med \mu=15.25 og \sigma=2.36) i intervallet [13,17].
Neden for ser du dette illustreret dels grafisk, og dels ved en beregning i Noter værkstedet:
Du kan også
lave denne arealbestemmelse
i Diagrammer og Statistik med 4:Undersøg data \rightarrow 5:Skraver under funktion, men her kan du ikke indtaste grænserne 13 og 17. De to grænser skal først afsættes ved at plotte dem som værdier med 8:Plot værdi.
\chi \, ^2-test for uafhængighed (med integraler)
I dette afsnit benyttes her integraler til at beregne den kritiske værdi og til fastlæggelse af p-værdien.
En forretningskæde vil undersøge, om farven på indpakningen af nye kartofler påvirker salget. Butikken sælger derfor i en periode poser med samme slags kartofler, alle med 2,5 kg/ pose og til samme pris.
Der bliver i alt sendt 600 poser kartofler ud i butikkerne, hvoraf 520 bliver solgt. Af de solgte poser er 375 gule, og der er 55 gule poser tilbage. De øvrige poser er blå.
Undersøg, om der er grundlag for at påstå, at farven påvirker salget af kartofler.
Først skal du lige vha. lidt hovedregning regne ud, at der er solgt 145 blå poser, og der er 25 blå poser tilbage. Indtast oplysningerne i et Lister og Regneark værksted:
Du skal afgøre, om de oplyste data er i rimelig overensstemmelse med nulhypotesen om uafhængighed mellem farve og antal solgte poser. Hertil skal du benytte den indbyggede test for uafhængighed af to variable. Testen kan klares direkte i Lister og Regneark.
Vælg 4:Statistik \rightarrow 4:Statistiske tests… \rightarrow 8:X2uafhængighedstest…. Guiden forventer, at du indtaster navnet på en matrix med observationerne. Dette kan du klare ved at indtaste {gul,blå}: tuborgklammer { og } kommer når man holder Shift+Alt 8 og Shift+Alt 9 inde.
Resultatet fra skærmbilledet til højre fremgår det at:
- \chi \, ^2 – teststørrelsen har værdien 0.38672
- p-værdien er 53.4%, dvs. sandsynligheden for at finde en teststørrelse, der er mindst lige så skæv som den observerede, er 53.4%. Nulhypotesen accepteres altså på signifikansniveauet 5%.
- Teststørrelsen er \chi \, ^2 – fordelt med 1 frihedsgrad.
De forventede værdier finder du i matricen ExpMatrix og enkeltbidragene til X2-teststørrelsen finder du i CompMatrix. Vil du se de to matricer, sker det nemmest i et Noter værksted, hvor de hentes via knappen eller blot skrives vha. stat.:
Du får ikke oplyst den kritiske værdi for en test på signifikansniveau 5%. Skal du bruge denne, må du selv beregne den. Du kan fx beregne kritiske værdi direkte fx i et Noter værksted som illustreret herunder:
En anden tilgang til denne opgave er at gå ind i Noter, hvor du selv skal definere matricen med de observerede værdier, men det klarer du nemt med skabelonen 2×2-marix 
.
Til beregningen skal du benytte funktionen \chi \, ^22way, som du finder i kataloget (husk, at Guider skal være slået til) eller 
6:Beregninger \rightarrow 6:Statistik \rightarrow :7:Statistiske tests \rightarrow 8 \chi \, ^2 uafhængighedstest…
Hvis du har indtastet gul og blå i Lister og Regneark, kan du definere obs ved obs:={gul,blå}
Normalfordeling: Konfidensinterval og hypotesetest
En kaffeautomat skal fylde 23 cl kaffe i et krus ved brygningen. Virksomheden, der producerer automaten, vil teste den, inden den sælges. Den mænge kaffe, automaten hælder i et krus, vides at være normalfordelt med middelværdi m og spredning \sigma=1.5 ml. For at teste automaten har man ladet den brygge 20 krus kaffe, og målt indholdet:
229.4\enspace 229.7\enspace 230.2\enspace 230.2\enspace 232.0\enspace 231.2\enspace 230.0\enspace 230.6\enspace 230.0\enspace 229.4
230.9\enspace 228.5\enspace 231.5\enspace 230.9\enspace 231.2\enspace 227.9\enspace 230.6\enspace 232.0\enspace 230.3\enspace 232.3
Find 90% konfidensintervallet for populationsmiddelværdien af den mænge kaffe, der serveres af automaten
Antyder ovenstående målinger, at populationsmiddelværdien er forskellig fra 230 ml?
Start med at indtaste måleresultaterne i en søjle i et Lister og Regneark værksted, og navngiv søjlen indhold. Indsæt et Diagrammer og Statistik værksted, indsæt indhold i pladsholderen langs x-aksen og vælg normalfordelingsplot som plottype:
Normalfordelingsplottet viser, at stikprøven på de 20 krus kaffe afspejler antagelsen om, at kaffeindholdet er normalfordelt.
I Lister og Regneark, vælg 4:Statistik \rightarrow 3:Konfidensintervaller… \rightarrow 1:z-interval for én middelværdi, og vælg Data i næste skærmbillede. Fyld ud som vist, og afslut med OK.
Her ser du, at konfidensintervallet er [229.888, 230.992]. Desuden fremgår, at stikprøve- middelværdien er x = 230.44 og at standardafvigelsen i stikprøven er s_x =1.1362.
For at besvare det andet spørgsmål, skal du teste hypotesen H_0:\, \mu=230 mod alternativet H_a:\, \mu \neq 230 på niveau 10%.
Da populationsmiddelværdien \mu ligger i 90% konfidensintervallet [229.888, 230.992], du fandt ovenfor, kan du ikke forkaste hypotesen H_0. Du kan dermed konkludere, at der ikke er noget der indikerer, at populationsmiddelværdien \mu er forskellig fra 230 ml.
Normalfordelingstest (σ kendt)
En anden mulighed for at udføre testen af normalfordelingen finder du i 
4:Statistik \rightarrow 4:Statistiske tests… \rightarrow 1:z-test for én middelværdi. Fyld ud som vist, og afslut med OK.
De fleste værdier på det sidste skærmbillede kender du allerede. De to nye, z og PVal, bruges til at afgøre, om en hypotese skal forkastes eller ej.
Teststørrelsen z er normalfordelt med middelværdi 0 og spredning 1. Da du skal teste på niveau 10%, vil kritiske værdier for z befinde sig i de to 5%-haler i normalfordelingen.
I det venstre skærmbillede ser du de to 5%-haler skraveret, og det fremgår, at teststørrelsen z ligger i acceptområdet.
På det højre skærmbillede er vist, hvad værdien PVal betyder: Hvis hypotesen forkastes, så er sandsynligheden for, at vi forkaster en sand hypotese ca. 18.96%.
Teststørrelsen z udregnes således z=\cfrac{\bar{x}-\mu_0}{\Big( \cfrac{\sigma}{\sqrt{n}}\Big)} hvor \bar{x} er stikprøve middelværdien og n er stikprøve størrelsen. Z er normalfordelt med middelværdi 0 og spredning 1.
Normalfordelingstest (σ ukendt)
En skole har undersøgt 25 elevers brug af skolens internet i en uge. Antallet af timer brugt på internettet i en uge blev registreret til:
5.0\enspace 4.4\enspace 5.7\enspace 5.6\enspace 5.5\enspace 5.2\enspace 5.0\enspace 4.8\enspace 3.6\enspace 4.1\enspace 4.6\enspace 4.9\enspace 4.0
6.7\enspace 5.5\enspace 5.4\enspace 6.7\enspace 5.8\enspace 5.4\enspace 4.8\enspace 5.9\enspace 5.1\enspace 3.8\enspace 4.1\enspace 6.7
Antag, at den tid, skolens elever (populationen) bruger på internettet i en uge er normalfordelt.
Find 95% konfidensintervallet for stikprøve-middelværdien.
Er der indikation for på niveau 5%, at skolens elever bruger mere end 5 timer på Internettet?
Indtast data i et Lister og Regneark værksted. Kald kolonnen tid, og beregn t-konfidensintervallet (præcis som du gjorde ved z-testen):
Her kan du se, at t-konfidensintervallet er [4.77418,5.48982].
For at besvare det andet spørgsmål, skal du teste hypotesen H_0: \, \mu=5 mod alternativet H_a: \, \mu>5 på niveau 5%.
Lav en t-test: 4:Statistik \rightarrow 4:Statistiske tests… \rightarrow 2:t-test for én middelværdi. Gå frem som ved z-testen, og indstil således:
Du kan således ikke forkaste hypotesen \mu=5 på det foreliggende grundlag.
Opinionsundersøgelser
Ved sidste folketingsvalg fik Dansk Folkeparti 12.3% af stemmerne. I en opinionsundersøgelse spørger man 800 tilfældigt udvalgte danskere med stemmeret, hvor de vil sætte deres kryds, hvis der var valg i morgen. Af de 120 adspurgte vil stemme på DF.
Giver dette resultat en indikation for, at DF har ændret vælgertilslutning?
Med TI-Nspire går den slags hypotesetest som en leg. Du kan fx starte med at finde konfidensintervallet. I Noter vælger du 6:Beregninger \rightarrow 6:Statistik \rightarrow 6:Konfidensintervaller… \rightarrow 5:z- interval for en andel…, og udfylder som vist:
Disse resultater viser, at stikprøveprocentdelen er 15% og at konfidensintervallet er [0.125257,0.174743]. Dvs., at med 95% sikkerhed, vil den sande procentdel for populationen vil ligge mellem 12.5% og 17.5%.
Hypotesen H_0: DF har uændret vælgertilslutning må altså forkastes på det foreliggende grundlag.