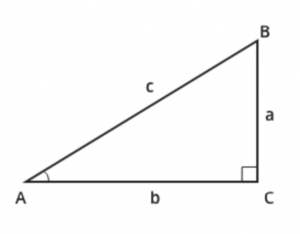
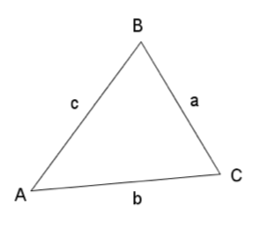
Retvinklede Trekanter
I den retvinklede trekant gælder Pythagoras’ sætning: a^2+b^2=c^2
Herunder beskrives simple formler med sinus, cosinus og tangens, som man kan bruge til at finde de ukendte sider og vinkler i en retvinklet trekant.
- Sinus til en vinkel er lig med den modstående katete, divideret med hypotenusen.
sin(A)=\cfrac{a}{c}
Dette kan omskrives til følgende hjælpeformel:
A=sin^{-1}\Big(\cfrac{a}{c}\Big)
- Cosinus til en vinkel er lig med den hosliggende katete, divideret med hypotenusen
cos(A)=\cfrac{b}{c}
Dette kan omskrives til følgende hjælpeformel:
A=cos^{-1}\Big(\cfrac{b}{c}\Big)
- Tangens til en vinkel er lig med den modstående katete, divideret med den hosliggende katete
tan(A)=\cfrac{a}{b}
Dette kan omskrives til følgende hjælpeformel:
A=tan^{-1}\Big(\cfrac{a}{b}\Big)
I TI-Nspire er der en kommando for sin^{-1}, cos^{-1} og tan^{-1}, og de kan skrives som hhv. arcsin, arccos og arctan i Nspire.
Vilkårlige Trekanter
I den vilkårlige trekant gælder både sinus- og cosinusrelationerne, som kan anvendes til at finde både sider og vinkler.
- Sinusrelationen
Ønsker man at finde en side, skal man anvende en af følgende sætninger:
\cfrac{a}{sin(A)}=\cfrac{b}{sin(B)}=\cfrac{c}{sin(C)}
Ønsker man derimod at finde en vinkel, skal man anvende en af følgende sætninger:
\cfrac{sin(A)}{a}=\cfrac{sin(B)}{b}=\cfrac{sin(C)}{c}
- Cosinusrelation
Ønsker man at finde en side, skal man anvende en af følgende sætninger:
a^2=b^2+c^2-2\cdot b\cdot c\cdot cos(A)
b^2=a^2+c^2-2\cdot a\cdot c\cdot cos(B)
c^2=b^2+a^2-2\cdot b\cdot a\cdot cos(C)
Ønsker man derimod at finde en vinkel, skal man anvende en af følgende sætninger:
cos(A)=\cfrac{b^2+c^2-a^2}{2\cdot b\cdot c}
cos(B)=\cfrac{a^2+c^2-b^2}{2\cdot a\cdot c}
cos(C)=\cfrac{a^2+b^2-c^2}{2\cdot a\cdot b}
Arealformlen
Indenfor trigonometrien findes der en smart måde at regne arealet af en trekant ud på, man skal blot kende to sider og den mellemliggende vinkel.
T=\cfrac{1}{2}\cdot a\cdot b \cdot sin(C)
Opgave Eksempler

To personer bestemmer en flods bredde vha. et målebånd og en vinkelmåler. De to personer står med 11 meters afstand og måler sigtevinklerne A og C til et træ på den anden side af oden. Vinkel A måles til 79° og vinkel C til 64° (se figur).
a) Bestem |BC|
b) Bestem flodens bredde, dvs. højden fra B i trekant ABC