Vektors koordinater
For vektorerne \vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} og \vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix} gælder det at
\vec{a}+\vec{b}=\begin{pmatrix}a_1+b_1\\a_2+b_2\\a_3+b_3\end{pmatrix}
\vec{a}-\vec{b}=\begin{pmatrix}a_1-b_1\\a_2-b_2\\a_3-b_3\end{pmatrix}
k\cdot \vec{a}=\begin{pmatrix}k\cdot a_1\\k\cdot a_2\\k\cdot a_3\end{pmatrix}
En vektor \vec{a}=\begin{pmatrix}1 \\ 4 \\ 2\end{pmatrix} indskrives i TI-Nspire på følgende måde a:=[1,4,2]
Vektor mellem to punkter
Hvis A(x_1,y_1,z_1) og B(x_2,y_2,z_2) er to punkter, er \vec{AB}=\begin{pmatrix}x_2-x_1 \\ y_2-y_1 \\ z_2-z_1\end{pmatrix}
Vektors længde
Længden af vektoren \vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} er |\vec{a}|=\sqrt{a^2_1+a^2_2+a^2_3}
Kommandoen i TI-Nspire er norm(a)
Skalarproduktet (prikproduktet)
Skalarproduktet af \vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} og \vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix} er \vec{a}\cdot \vec{b}=a_1\cdot b_1+a_2\cdot b_2+a_3\cdot b_3
Kommandoen i TI-Nspire for skalarproduktet er dotP(a,b)
Hvis skalarproduktet er 0, vil det sige, at vektorerne danner en ret vinkel, \vec{a}\cdot \vec{b}=0 \leftrightarrow \vec{a} \bot \vec{b}
Afstand mellem to punkter
Hvis A(a_1,a_2,a_3) og B(b_1,b_2,b_3) er to punkter, er afstanden mellem dem bestemt ved |AB|=|\vec{AB}|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2}
Vinklen mellem vektorer
Vinklen v mellem de egentlige vektorer \vec{a} og \vec{b} er givet ved
cos(v)=\cfrac{\vec{a}\cdot \vec{b}}{|\vec{a}|\cdot |\vec{b}|}
For at finde vinklen direkte i TI-Nspire bruges sammensætningen af kommandoerne: arccos(dotP(a,b)/(norm(a)*norm(b)))
Linjens parameterfremstilling
En parameterfremstilling for linjen gennem punktet (x_0,y_0,z_0) med retningsvektoren \vec{r}=\begin{pmatrix}r_1\\r_2\\r_3\end{pmatrix}, er
\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}+t\cdot \begin{pmatrix}r_1\\r_2\\r_3\end{pmatrix} \qquad eller \qquad \begin{matrix}x=x_0+t\cdot r_1 \\ y=y_0+t\cdot r_2 \\ z=z_0+t\cdot r_3 \end{matrix}
Planer
En ligning for den plan \alpha, som går gennem punktet P_0=(x_0,y_0,z_0), og som har normalvektoren \vec{n}=\begin{pmatrix}a\\b\\c\end{pmatrix}, er
a(x-x_0)+b(y-y_0)+c(z-z_0)=0
Vektorprodukt (krydsprodukt)
Vektorproduktet for to vektorer \vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} og \vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix} er vektoren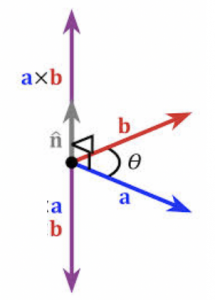
\vec{a}\times \vec{b}=\begin{pmatrix}d_{23}\\d_{31}\\d_{12}\end{pmatrix}=\begin{pmatrix}\begin{vmatrix}a_2 & a_3 \\ b_2 & b_3\end{vmatrix}\\[1em]\begin{vmatrix}a_3 & a_1 \\ b_3 & b_1\end{vmatrix}\\[1em]\begin{vmatrix}a_1 & a_2 \\ b_1 & b_2\end{vmatrix}\end{pmatrix}
Kommandoen i TI-Nspire er crossP(a,b)
Er \vec{a} og \vec{b} egentlige vektorer gælder at \vec{a}\times \vec{b}=0 \Leftrightarrow \vec{a}||\vec{b}
Den numeriske værdi af \vec{a}\times \vec{b} er arealet af det parallelogram, som \vec{a} og \vec{b} udspænder.
Afstand mellem punkt og plan
Afstanden fra punktet P_1(x_1,y_1,z_1) til planen \alpha med ligningen a\cdot x+b\cdot y+c\cdot z=0 er dist(P_1,\alpha)=\cfrac{|a\cdot x_1+b\cdot y_1 +c\cdot z_1+d|}{\sqrt{a^2+b^2+c^2}}
Kommandoen i TI-Nspire ville være følgende abs(a*x_1+b*y_1+c*z_1+d)/sqrt(a^2+b^2+c^2)
Indtastet i TI-Nspire er afstanden fra linjen 2\cdot x-3\cdot y+4\cdot z+1=0 til punktet (5,6,-7), følgende abs(2*5+(-3)*6+4*(-7))/sqrt(2^2+(-3)^2+4^2)
Vinkel mellem planer
En vinkel mellem to planer er vinklen mellem deres normalvektorer.
Vinkel mellem linje og plan
Den spidse vinkel v mellem en linje med retningsvektor \vec{r} og en plan med normalvektor \vec{n} er bestemt ved
v= \Big\{ \begin{matrix}90^\circ-w \enspace \text{hvis}\enspace o^\circ \leq w \leq 90^\circ \\ w-90^\circ \enspace \text{hvis}\enspace 90^\circ \leq w \leq 180^\circ \end{matrix}
w findes som vinklen mellem \vec{r} og \vec{n}.
Kuglens ligning
Den følgende ligning kaldes kuglens ligning: (x-a)^2+(y-b)^2+(z-c)^2=r^2, hvori (a,b,c) er cirklens centrum, og r radius.
Bemærk fortegnet foran tallene i parenteserne. Når koordinaten fra centrum er positiv, står der et minus i parentesen og omvendt.
Tangentplan til kuglen
Hvis P_0(x_0,y_0,z_0) er et punkt på kuglen med centrum i (a,b,c), er en ligning for tangentplanen i P_0
(x_0-a)\cdot(x-x_0)+(y_0-b)\cdot(y-y_0)+(z_0-c)\cdot(z-z_0)=0