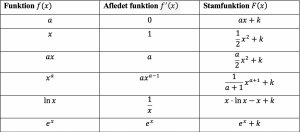
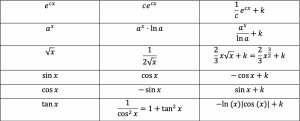
Afledede og stamfunktioner
Det er enormt vigtigt at regne de sidste tre ovenstående funktoner i radianer.
Tangentens ligning
Ligningen for tangenten t til grafen for f i P(x_0,y_0) er y=f'(x_0)\cdot (x-x_0)+f(x_0)
I TI-Nspire findes tangentens ligning med betingelsen x_0=2 med kommandoen: tangentLine(f(x),x,2)
Regneregler for differentiation
Hvis f og g er differentiable i x_0, er f+g, f-g, f\cdot g, \cfrac{f}{g} og k\cdot f differentiable i x_0, og differentialkvotienterne er:
(f+g)'(x_0)=f'(x_0)+g'(x_0)\qquad \qquad \qquad \qquad (f-g)'(x_0)=f'(x_0)-g'(x_0)
(f\cdotg)'(x_0)=f'(x_0)\cdot g(x_0)+f(x_0)\cdot g'(x_0)\qquad \qquad (\cfrac{f}{g})'(x_0)=\cfrac{f'(x_0)\cdot g(x_0)-f(x_0)\cdot g'(x_0)}{g(x_0)^2}
\qquad \qquad \qquad(k \cdot f)'(x_0)=k\cdot f'(x_0) \qquad \qquad \qquad (f\circ g)'(x_0)=f'(y_0)\cdot g'(x_0)=f'(g(x_0))\cdot g'(x_0)
Regneregler for det ubestemte integral
For ubestemte integraler gælder følgende regneregler. \int f(x)dx=F(x)+k hvor F(x) er en stamfunktion til f(x)
De første to regler siger, at man må integrere en sum eller en differens af funktioner ved at integrere de enkelte led hver for sig.
\int f(x)+g(x)dx=\int f(x)dx+\int g(x)dx\qquad \qquad \qquad \qquad \int f(x)-g(x)dx=\int f(x)dx-\int g(x)dx
Den sidste regneregel tillader at man sætter en konstant uden for integraltegnet.
\int k\cdot f(x)dx= k\cdot \int f(x)dx
Herunder ses integration ved substitution hvilket er en metode, som man kan bruge til at omskrive et integrale til noget, der er lettere at have med at gøre.
\int f(g(x))\cdot g'(x)dx=\int f(t)dt=F(t)+k=F(g(x))+k hvor t=g(t), og F er en stamfunktion til f.
Regneregler for det bestemte integral
Ligesom de ubestemte integraler er der tilsvarende regneregler for bestemte integraler. \int_{a}^{b}f(x)dx=[F(x)]^{a}_{b}=F(b)-F(a) hvor F(x) er en stamfunktion til f(x)
De første to regler siger, at man må integrere en sum eller en differens af funktioner ved at integrere de enkelte led hver for sig.
\int_{a}^{b} f(x)+g(x)dx=\int_{a}^{b}f(x)dx+\int_{a}^{b}g(x)dx\qquad \qquad \qquad \qquad \int_{a}^{b} f(x)-g(x)dx=\int_{a}^{b} f(x)dx-\int_{a}^{b} g(x)dx
Den sidste regneregel tillader at man sætter en konstant uden for integraltegnet.
\int_{a}^{b} k\cdot f(x)dx=k\cdot \int_{a}^{b}f(x)dx
Hvis integrationsintervallet for en kontinuert funktion f er [a;b], kan det deles op i to intervaller så som [a;c] og [c;b], og integrationen kan foretages i hvert interval særskilt. Dette kaldes indskudsreglen, som er illustreret i nedenstående ligning:
\int_{a}^{b} f(x)dx=\int_{a}^{c}f(x)dx+\int_{b}^{c}f(x)dx
Ligesom ved ubestemte integraler er det muligt at bruge integration ved substitution til at beregne bestemte integraler. Integration ved substitution ses herunder:
\int_{a}^{b} f(g(x))\cdot g'(x)dx=\int_{g(a)}^{g(b)}f(t)dt hvor t=g(x)
Rumfang
Hvis f er kontinuert og ikke-negativ i [a;b] er rumfanget V af det omdrejningslegeme, der fremkommer, når grafen for f drejes 360^\circ om x-aksen, bestemt ved
V=\pi \int_{a}^{b}f(x)^2dx
Kurvelængden s af f i intervallet er bestemt ved
s=\int_{a}^{b}\sqrt{1+f'(x)^2}dx
Grænseværdier
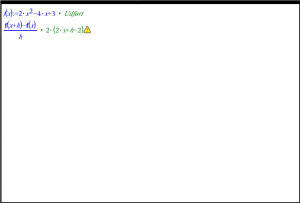
En funktion f er givet ved f(x)=2\cdot x^2-4\cdot x+3. Bestem grænseværdien af differensbrøken for f, når h går mod 0.
Først defineres funktionen f i Noter ved f(x):=2\cdot x^2-4\cdot x+3 og beregn differensbrøken:
Grænseværdier bestemmer du vha.
Man skal enten indsætte skabelonen 
, eller brug kommandoen lim(,,). En af pladsholderne i skabelonen er grå — det betyder, at det er valgfrit, om du skriver noget i denne.
Differentialregning
Differentialkvotienter bestemmer du vha. skabelonen 
, eller ved brug af kommandoen d(,). Først indtaster du, hvilken variabel der skal differentieres med hensyn til, og dernæst det udtryk, der skal differentieres. På skærmbilledet herunder kan du se nogle eksempler:
I det følgende eksempel er det fornuftigt at definere en ny funktion ved:
fp(x):=\frac{d}{dx}(f(x))
Så vil fp altid rumme den afledede af funktionen f, og f kan jo skifte indhold. Herefter kan du arbejde med fp som med enhver anden funktion. Det illustreres i eksemplet herunder.
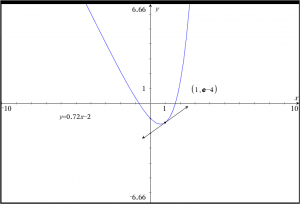
En funktion f er givet ved forskriften:
f(x)=e^x-2\cdot x-2
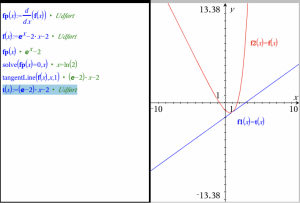
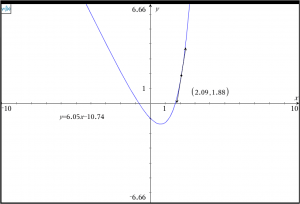
Bestem de punkter, hvor fhar en vandret tangent, og bestem tangentligningen i punktet med førstekoordinaten 1.
Første del klares ved at løse ligningen f'(x)=0. Til den anden del, skal du benytte kommandoen tangentLine(f(x),x,1), der umiddelbart giver dig et funktionsudtryk for tangenten til grafen for f i punktet med x-koordinaten 1.
I sidste linje er det vist, hvordan tangenten kan defineres som en funktion af x. Opgaven er løst i en opsplittet skærm med et Noter værksted til venstre og et Graf værksted til højre.
Dynamisk tangent
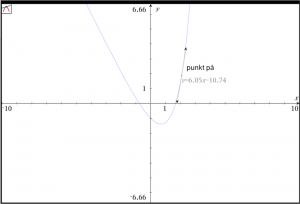
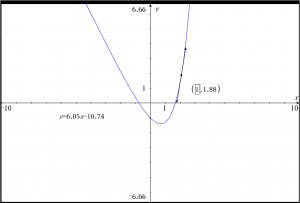
I Graf værkstedet finder du et stærkt tangentværktøj, hvormed du kan klistre en dynamisk tangent på en graf. Først tegnes en graf for f i Grafværkstedet. Vælg herefter 
8:Geometri \rightarrow 1:Punkter og linjer \rightarrow 7:Tangentlinje. Klik i et punkt på grafen, og en tangent tegnes i dette punkt — skærmbilledet herunder viser situationen umiddelbart før punktet placeres:
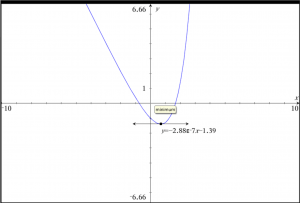
Grib punktet, og træk det langs kurven:
Passerer du interessante punkter undervejs, så bliver du underrettet.
Du kan få vist tangentens ligning og punktets koordinater således: Vælg 
1:Handlinger \rightarrow 8:Koordinater og ligninger. Klik på punktet og tangenten, og flyt tangentligningen passende.
Du kan ændre punktets koordinater direkte:
Du ændrer en koordinat ved at dobbeltklikke på den, og indtaste den nye værdi.
Integralregning
Stamfunktioner bestemmer du ved at benytte skabelonen 
, eller ved at bruge kommandoen \int(,)
Først indtaster du, hvilket udtryk der skal integreres, og dernæst den variabel der skal integreres med hensyn til. Her ser du nogle eksempler:
Opgave eksempler med ubestemte integraler
En funktion f er bestemt ved f(x)=3\cdot x^2-21\cdot x+30.
a) Bestem den stamfunktion til f, der går gennem punktet .
Start med at definere f. Du kan ikke benytte navnet F for en stamfunktion til f, da TI- Nspire ikke skelner mellem store og små bogstaver i variabelnavne. Brug fx navnet sf i stedet.
Når du bruger skabelonen til at bestemme stamfunktioner, får du ikke en integrationskonstant med i resultatet — den må du selv tilføje. Du skal derfor definere stamfunktionen ved:
sf(x)=\int f(x)dx+k
Opgaven er løst på nedenstående skærmbillede:
Opgave eksempler med bestemte integraler
Til det bestemte integral benytter du skabelonen 
, eller kommandoen \int(,,,). Du udfylder som ved det ubestemte integral — blot skal du her medtage grænser. Husk, at du navigerer hurtigst mellem pladsholderne med TAB.
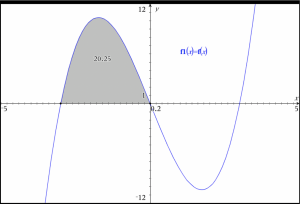
Grafen for f(x)=x^3-9\cdot x afgrænser sammen med x-aksen i anden kvadrant en punktmængde.
a) Bestem arealet af denne punktmængde.
På det højre skærmbillede ser du opgaven løst grafisk. Først indtastes f(x) og derefter kan grafen undersøges med 
6:Undersøg grafer \rightarrow 7:Integral. Med dette værktøj skal du først udpege funktionen og dernæst de to skæringspunkter med x-aksen en efter en — du kan også indtaste grænserne direkte.
Bestem først skæringspunkterne med x-aksen ved at bruge værktøjet til bestemmelse af skæringspunkter (udpeg x-aksen som den ene graf).